CSCB315 Увод в алгоритмите и програмирането

Info

Записки от лекции по “CSCB214 Увод в алгоритмите и програмирането” към НБУ, водени от проф. д-р Велина Славова и гл. ас. д-р Филип Андонов.

Общи §

Алгоритъмът е такова крайно, дискретно (постъпково), детерминирано преобразование, което, приложено над произволен допустим набор от стойности на входното множество, довежда до получаването на единствен набор от допустими стойности на изходното множество.

• Дискретност - преобразуването на входа в изход става на стъпки. Всяка стъпка е отделно елементарно действие над елементи на Средата, водещо до промяна на стойностите им.
• Детерминираност - Елементите на Средата са дефинирани. Последователността на изпълнение на стъпките е определена по единствен начин. Всяка елементарна стъпка се извършва по точно определено правило, по единствен начин. В резултат, задаването на конкретни стойности на входа води до получаване на единствен “изход”.
• Крайност - Елементите на Средата са краен брой. Преобразованието на входа в изход завършва след краен брой стъпки.
• Резултативност (ефективност). Всяка стъпка е изпълнима в момента, в който предписанието изисква това. Алгоритъмът е изпълним за обозримо време.

Инверсия: Редица от елементи, които не са наредени в естествен ред.

Пример:

• (4, 3) - 1 инверсия
• (5, 6, 2) - 2 инверсии (5, 2) и (6, 2)

Максимален брой инверсии в редица с елемента:

За редица наредена обратно на естествен ред. За първия елемент инверсиите са: , за втория елемент са , за третия елемент са и т.н.

Конструкции за управление §

• Клонове
  • байпас (if)
  • двуклон (if / else)
• Повторения
  • цикъл с предусловие
  • цикъл със следусловие
  • цикъл с вграден брояч

Събиране на две цели положителни числа §

Домашна работа №1. Дадени са две входни числа и и дефинираме две променливи, които ще съдържат резултата и - брояч. На присвояваме стойността на едното входно число - и изпълняваме цикъл с предусловие . В тялото на цикъла добавяме единица към и .

Домашна работа №2. Числата, с които работи алгоритъма са 0110 и 0011. В тялото на цикъла се използва всяко поредно число, отзад напред, за да работи с десетици, стотици, т.н. (в зависимост от бройната система). На всяка нова позиция на резултатното число C[k] записваме остатъка от деленето на от сумата на двете цифри от входните числа на “основата”, т.е. ако цифрите са 8+7 = 15, бройната система е 10 - C[k] ще съдържа . В carry променливата поставяме “колко пъти основата - (бройната система)” се съдържа в сумата на двете цифри, (“1 на ум :)”).

Написания алгоритъм в домашната работа трябва да ползва цикъл с вграден брояч, а не цикъл с предусловие. В C++ имплементацията, броячът просто трябва да бъде дефиниран извън for() декларацията, за да е достъпен за последната стъпка - добавяне на последното “на ум”. Въпреки че съм се опитала да напиша алгоритъм, който да работи за много бройни системи, ако системата надхвърля “десет” (повече от 10 цифри/букви, например 12) - не работи. 🤷

Алгоритъм на Евклид §

Алгоритъм за намиране на най-голям общ делител (НОД / GCD) на две естествени числа.

Трябва поне едно от числата да е различно от 0.

Взимаме двете входни числа и , проверяваме дали е равно на 0.

• Ако да, числото е търсеният най-голям общ делител.
• Ако не, повтаряме процеса, като използваме за входни данни и остатъка, получен при деленето на на ().

Препълване на числа §

Препълване (overflow) на числа се получава, когато аритметична операция дава за резултат число, чиито брой цифри са извън границите, които могат да бъдат използвани / показвани / записвани. Границите зависят от архитектурата на процесора и колко е голям регистъра на процесора, измерва се в битове, т.е. един 64-битов процесор, може да работи с числа до .

Точност на решението §

Домашна работа №4 Изчисляването на се прави дотогава, докато разликата между две последователни стойности е по-малка от 0.001 (или друга стойност), защото в компютрите не може да се представят рационалните числа и не могат да бъдат сравнявани надеждно (едното число може да бъде сметнато с грешка и т.н.).

Формула на Гаус за сумата на числа от 1 до n §

Доказателство (Гаус):

Записано в нарастващ ред

Записано в намаляващ ред

Събираме двете уравнения

се повтаря пъти

Изчисляване на sin(x) - Серии на Маклорен §

Сложност на алгоритъм §

Big O - - за най-лош случай. Big Theta - - за среден случай.

Обратното на e .

• - константно - взимане/писане на данни в масив, на базата на ключ
• - линейно време - намиране на най-малко/най-голямо число в масив; търсене на елемент чрез обхождане; броя операции, в най-лошия случай, е равен на броя елементи в масив;
• - логаритмично време, основа 2 - пример binary search, при , броя операции, за откриване на елемент е .
• - квадратично време - bubble sort / insertion sort; броя операции е ; напр. вложени 2 цикъла
• - факториел време - генериране на всички пермутации на елементите в даден масив

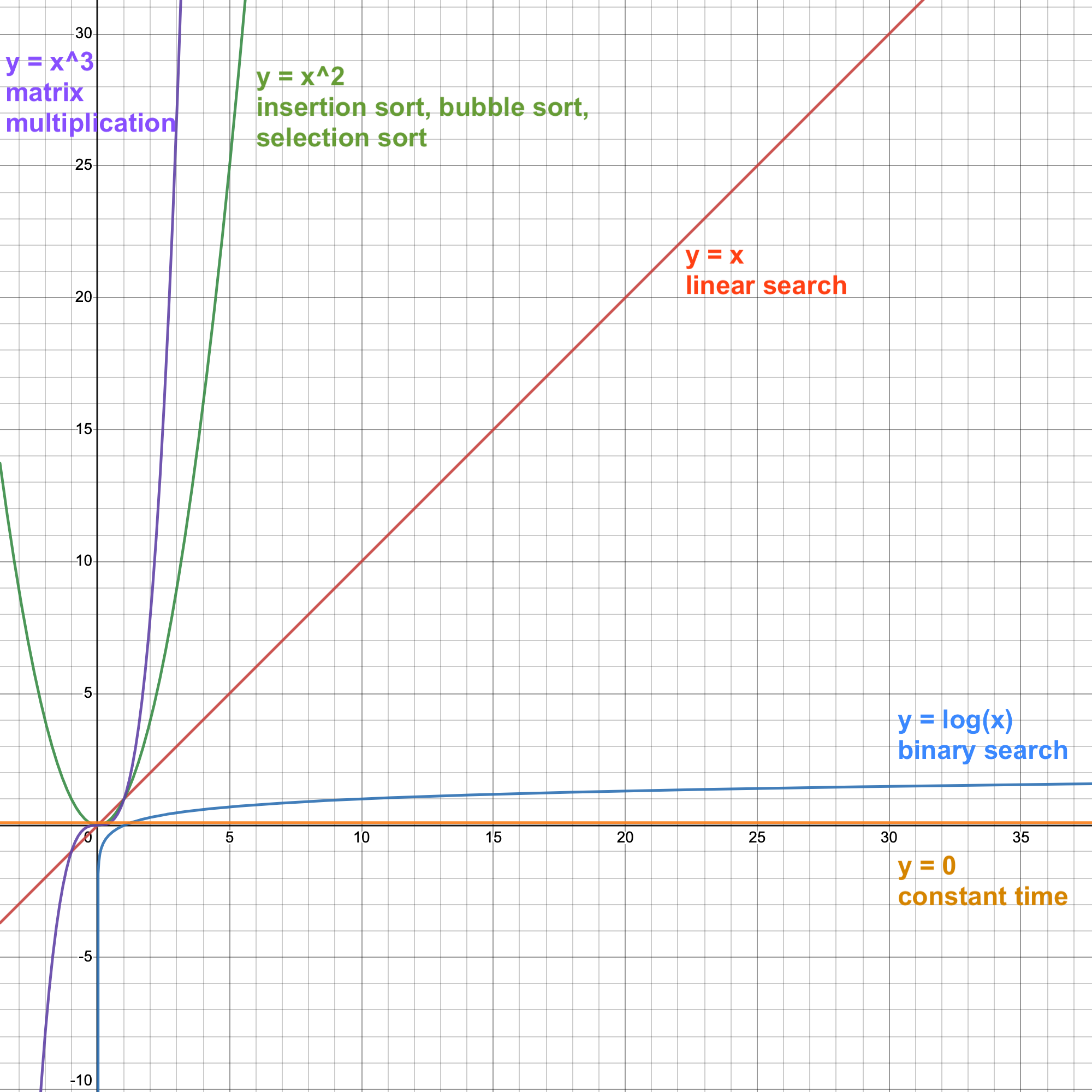
Алгоритми за претърсване §

Намиране на най-малка/най-голяма стойност §

Брой сравнения:

Linear search / Обхождане на всички елементи веднъж §

Максимум брой операции, нужни за намирането на елемент:

Броя операции се увеличава линейни с големината на подадения вход.

Графиката представлява диагонална линия започваща от (0, 0): .

Сложност:

Код за “Претърсване чрез обхождане”

Binary Search / Дихотомично търсене §

Максимум брой операции, нужни за намирането на елемент:

Броя операции нужни е логаритъм от големината на подадения вход (пр. брой елементи)

Домашна работа №5 Средата може да бъде намерена и като се промени “изчисляването на средата” на index = (lowerBound + upperBound) / 2.

Сложност:

Код за “Дихотомично търсене”

Алгоритми за сортиране §

Сортиране в друг масив §

Намира се най-голямата стойност на входния масив, запазва се в променлива и се поставя на последно място в “другия масив” (резултатния). Обхождаме входния масив, намираме минималната стойност и я поставяме на най-малката незаета позиция в резултатния масив. Минималната стойност от входния масив бива заменена с най-голямата стойност - дезактивираме.

Сложност:

Брой сравнения:

Метод на “Пряка селекция” §

Selection sort

Обхожда се масива и задаваме, че текущия елемент (и неговия индекс) е най-малкото число. Във вложен цикъл, обхождаме “следващите” елементи след текущия елемент (на външния цикъл), ако елемент от вложения цикъл бъде намерен като по-малък от вече зададения (във външния цикъл), заменяме променливите, които пазят индекса и стойността на най-малкия елемент.

След приключване на вложения цикъл разменяме стойностите на текущия елемент за външния цикъл и намерената най-малка стойност.

Сложност:

Брой сравнения:

Код за “Пряка размяна”

Метод на “Пряка размяна” / “Мехурчето” §

Bubble sort

Външният цикъл е цикъл със след-условие и се изпълнява, докато във вътрешният цикъл няма повече инверсии. Като се намери инверсия между съседни елементи, разменяме двата елемента. Вътрешния цикъл се изпълнява до дължината на елементите - брояч - 1, за да се избегне обхождане на вече “наредената част”.

Алгоритъмът нарежда масива “отзад-напред”, т.е. частта с “най-големи” елементи първо (в низходящ ред). Ако максималния елемент е в началото на масива, той ще бъде “избутан” (сменена позицията с всеки следващ елемент от итерацията) от вътрешния цикъл “нагоре” (към края на масива) като мехурче :)

Сложност:

• Най-лош случай:
• Най-добър случай:

Брой сравнения:

• Най-лош случай:
• Най-добър случай:

Код за “Пряка размяна”

Метод на “Пряко вмъкване” §

Insertion sort

Външен цикъл с броя, който обхожда всички елементи на даден масив. Вътрешния цикъл с условие се изпълнява, докато предходните елементи (спрямо текущия елемент на външния цикъл) имат инверсия в съседство a[j-1] > a[j]. Ако съседните елементи имат инверсия, техните стойности се разменят и продължва изпълнението на вътрешния цикъл “надолу” (към началото на масива).

Сложност:

• Най-лош случай:
• Най-добър случай:

Брой сравнения:

• Най-лош случай:
• Най-добър случай:

Код за “Пряко вмъкване”

Матрици §

Умножение §

При умножение на матрици и :

• се умножава ред от по колона от
• операцията не е комутативна (не може да се разменят местата на матриците)
• изходната матрица е с размер
• броя редове на трябва да отговаря на броя колони на
• броя умножения е
• броя събирания е

Сложност: (квадратна матрица)

Брой операции:

• Умножения:
• Събирания:

Решаване на СЛУ §

• Елементарни операции над ред/колона:
  • Смяна на ред/колона с друг ред/колона
  • Умножение на ред/колона с друг ред/колона
  • Събиране на два реда/колони

Алгоритмично метода на Гаус се прилага по следния начин:

• Разделяме реда, на който сме на коефициента, който е пред “първия” елемент от този ред (т.е. ако сме на първи ред - първия елемент, ако сме на втори ред - втория елемент)
• “Нулираме” всички останали елементи в колоната “под” елемента, на който сме взели коефициента, като изваждаме реда, върху който работим от всеки следващ като умножаваме единицата с коефициента, който “нулираме”
• Повтаряме действието колкото реда има матрицата / колкото неизвестни има СЛУ

СЛУ няма решение, ако лявата част е само 0 (коефициентите), а дясната не е 0 (константи).

 
int main() {  
    int n = 3;  
    float a[3][3] = {  
            {-3.0, -1.0, 2.0},  
            {2.0,  1.0,  -1.0},  
            {-2.0, 1.0,  2.0}  
    };  
    float b[] = {-11.0, 8.0, -3.0};  
    
	// function that just prints the matrix's rows & lines
    print_matrix(a, 3);
  
    for (int i = 0; i < n; ++i) {  
	    // element on the diagonal  
        float first_element = a[i][i]; 
        b[i] /= first_element;  
        for (int j = i; j < n; ++j) {  
            a[i][j] /= first_element;  
        }  
  
        // for the next rows (below)  
        for (int k = i + 1; k < n; ++k) {  
            // how many times this row needs to be subtracted  
            // from the current (i) row to zero its elements            
            float row_coefficient = a[k][i];  
            // only elements after the diagonal element  
            // of the current row            
            for (int l = i; l < n; ++l) {  
                a[k][l] = a[k][l] - row_coefficient * a[i][l];  
            }  
            b[k] = b[k] - row_coefficient * b[i];  
        }  
    }  
  
    std::cout << std::endl;  
    print_matrix(a, n);  
}